Was ist den die Binäre Suche?

Die Binäre Suche ist ein effizienter Algorithmus zur Suche nach einem Element in einer sortierten Liste. Sie funktioniert, indem sie den Suchbereich halbiert und feststellt, ob das gesuchte Element in der oberen oder unteren Hälfte liegt, was den Suchprozess im Vergleich zur linearen Suche erheblich beschleunigt. Wir finden die binäre Suche auch unter anderen folgenden Namen:

• Binary Search
• Interval Search
• Logarithmic Search
• Binary Chop

Du bist eher der Video Typ?

Dann schau dir doch das YouTube Video dazu an!

Achtung halt wie was?

Schalten wir noch einmal einen Gang zurück für alle, die wenig Berührung mit Algorithmen hatten. Schauen wir uns also folgendes Beispiel an: Wir haben eine lineare Suche. Auf gut Deutsch durchsuchen wir eine geordnete Datenstruktur, in unserem Fall ein Array. Dazu verwenden wir eine Schleife. Sehen wir uns die Animation unter dem Text an:

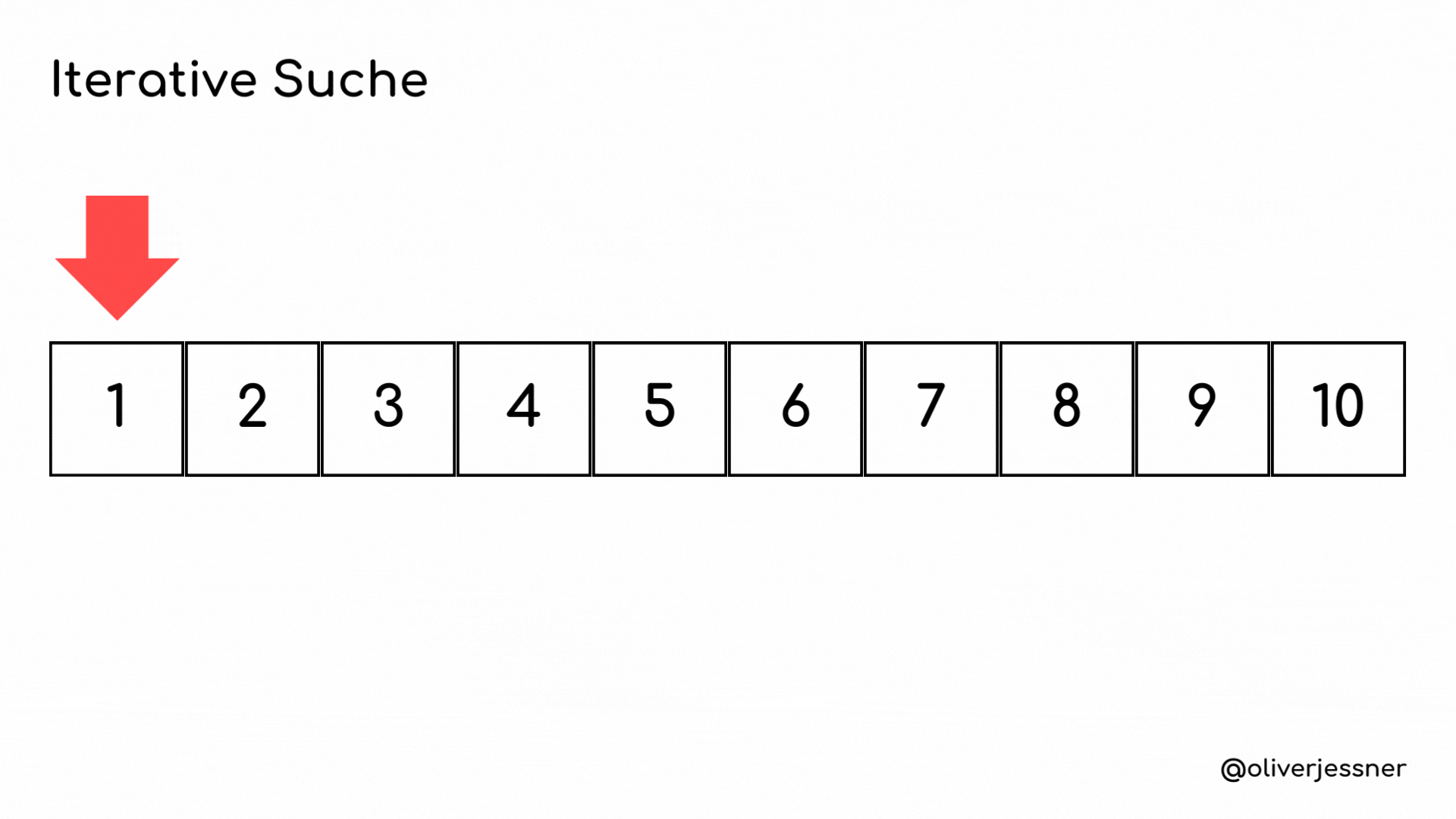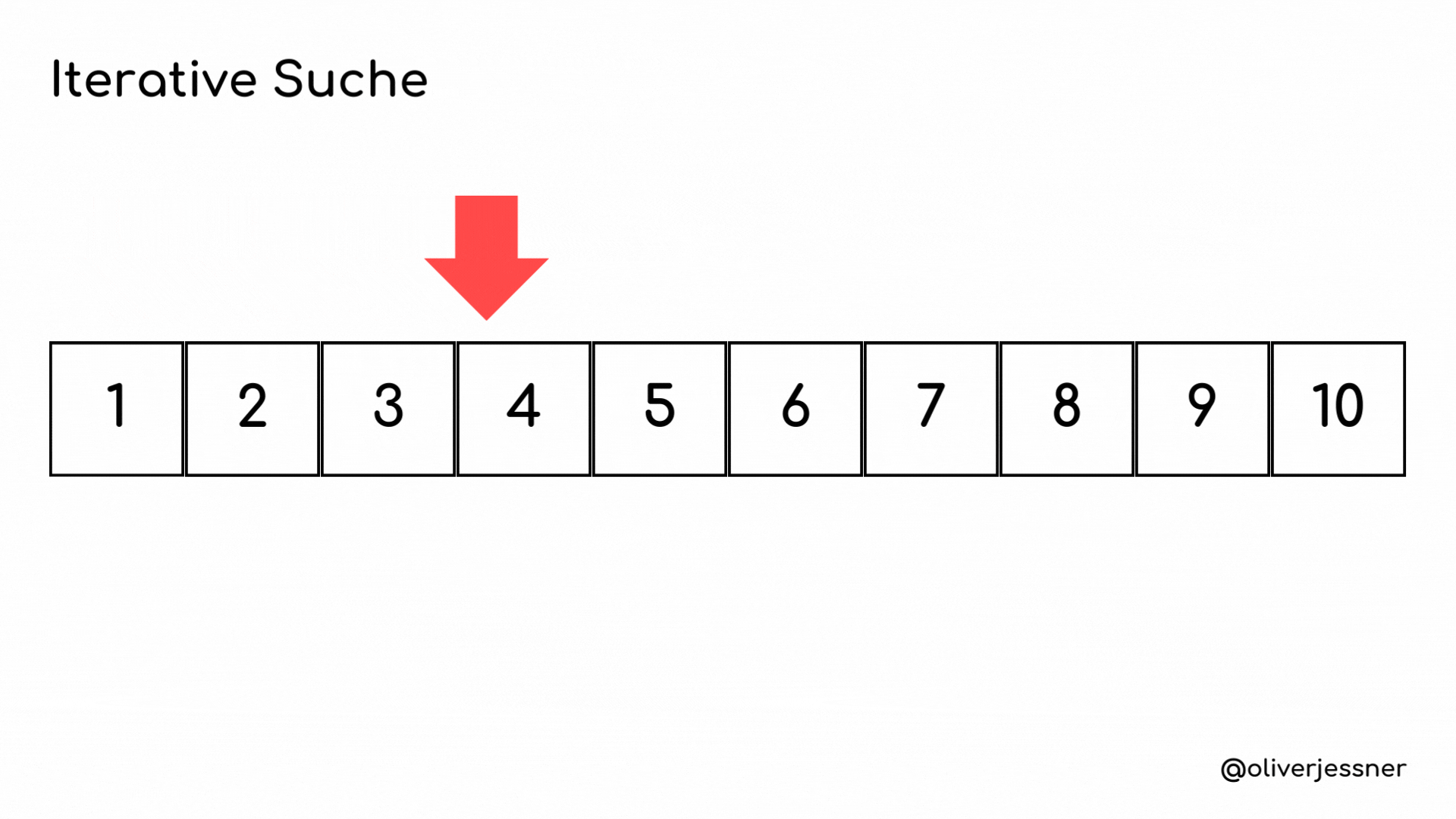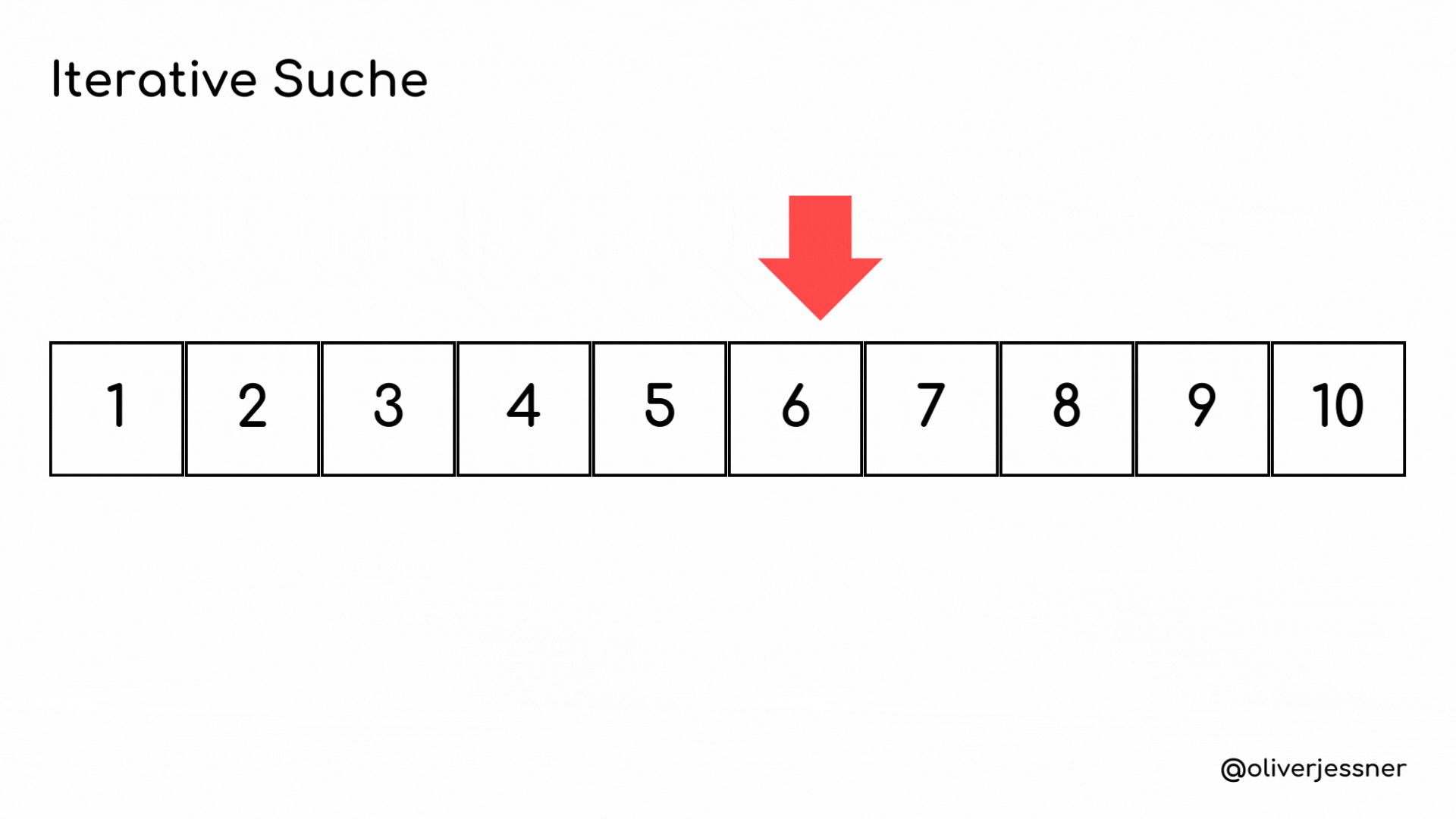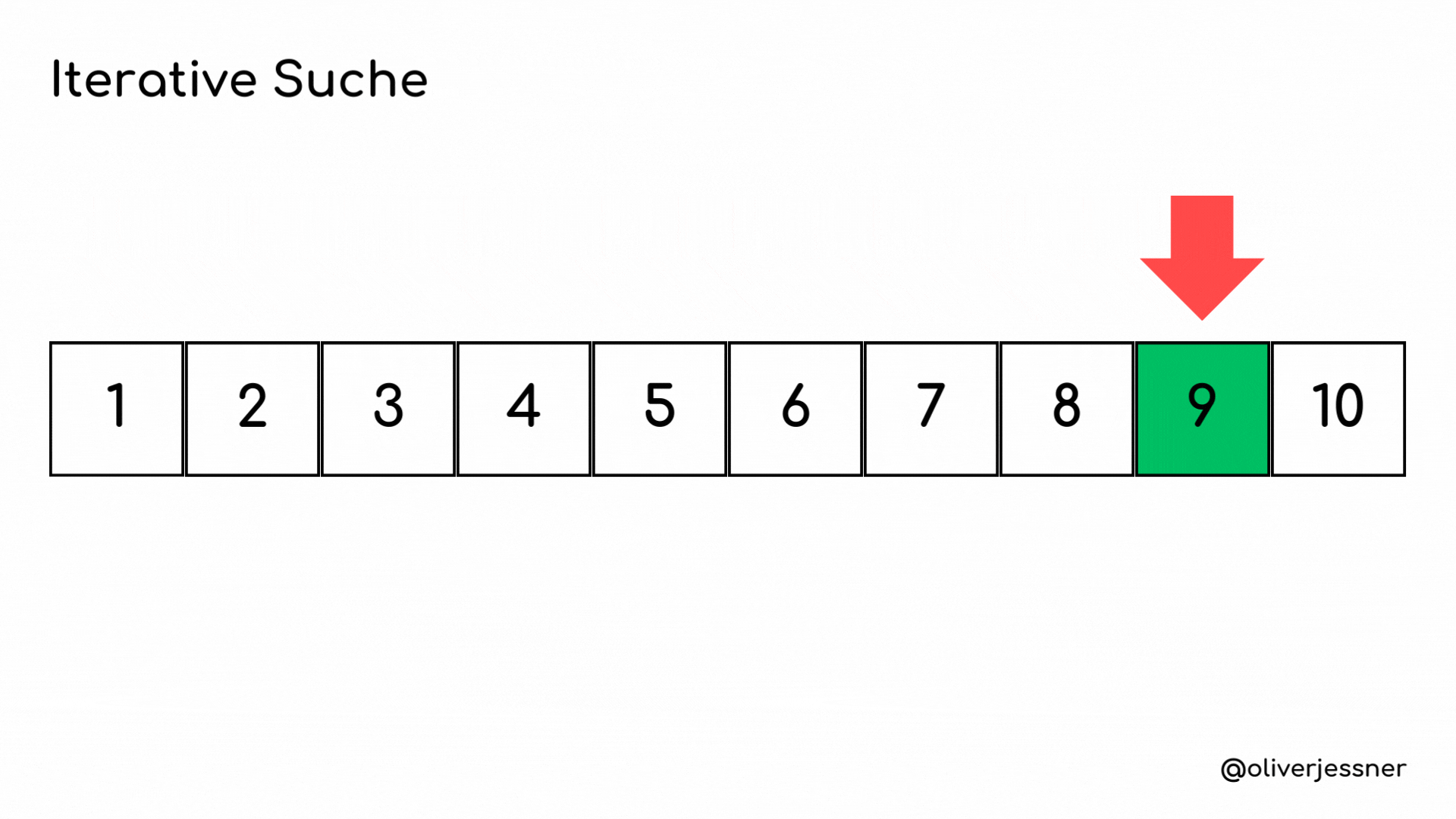
Man kann gut beobachten, dass dieser Suchalgorithmus etwas langsam sein kann. Stellen wir uns vor, wir haben ein Array mit 10 Millionen Elementen, und wir müssen etwas finden, das sich an Position 9 Millionen befindet. Das bedeutet, wir müssen 9 Millionen durchgehen, was lange dauern kann.

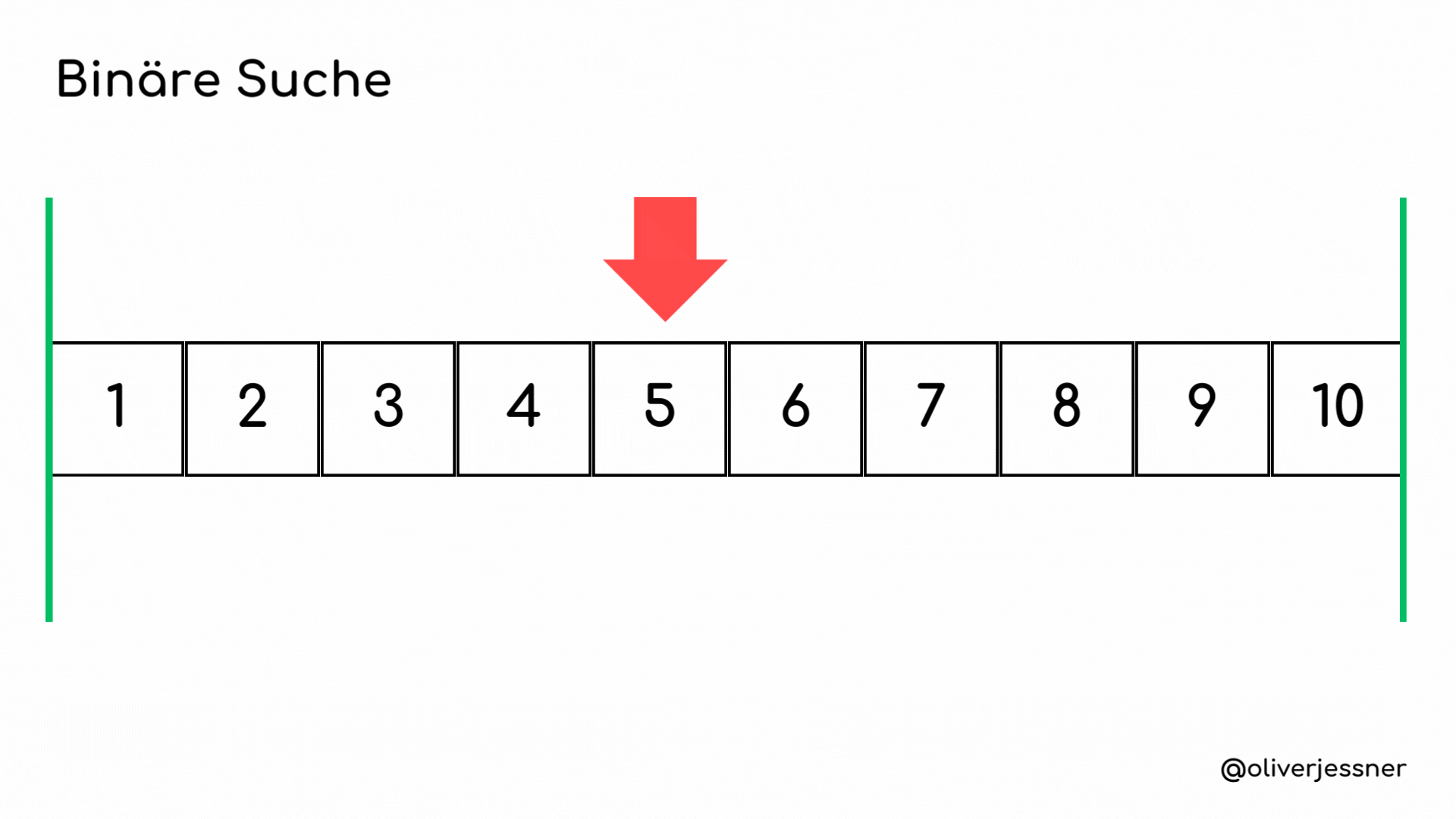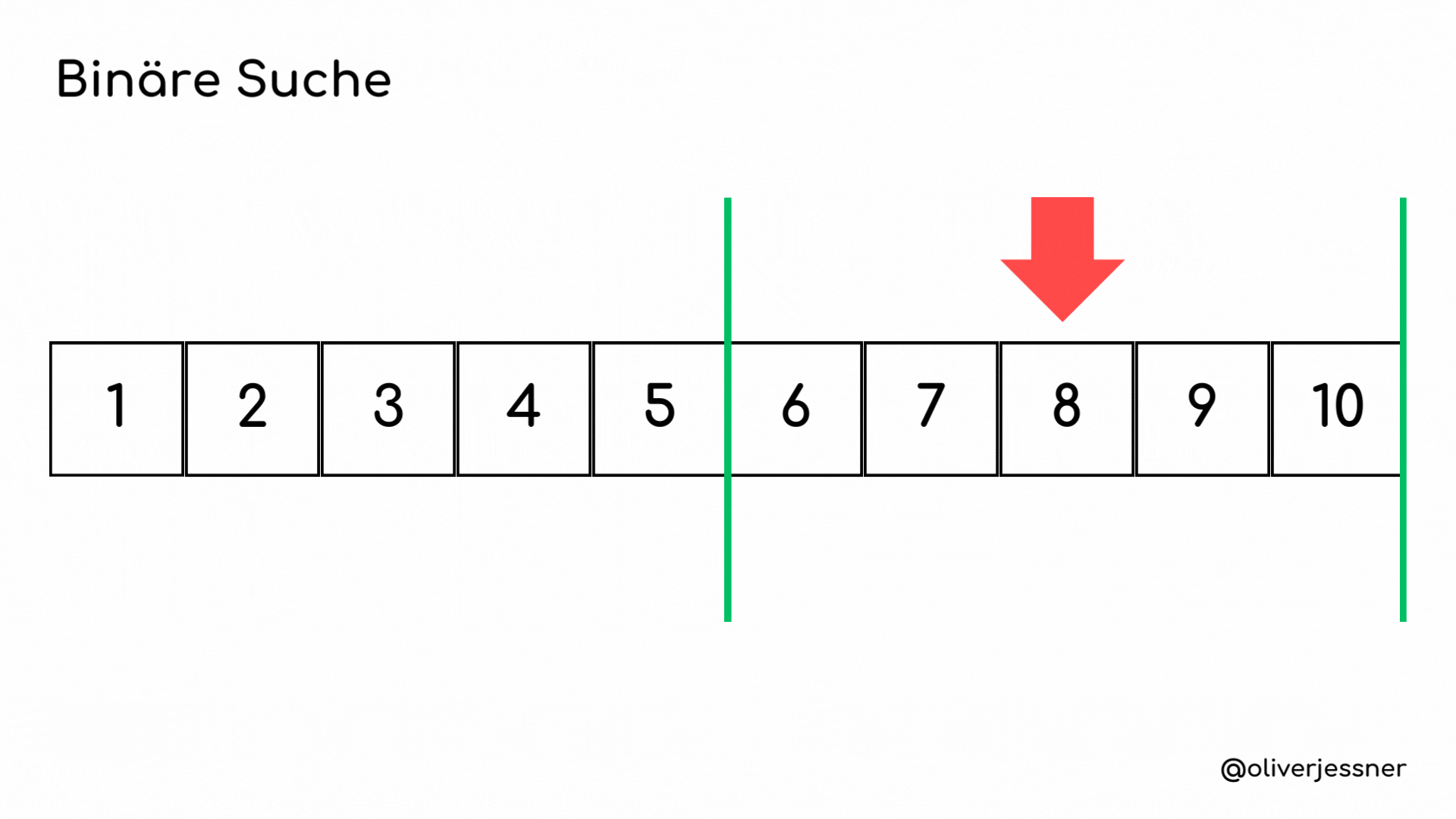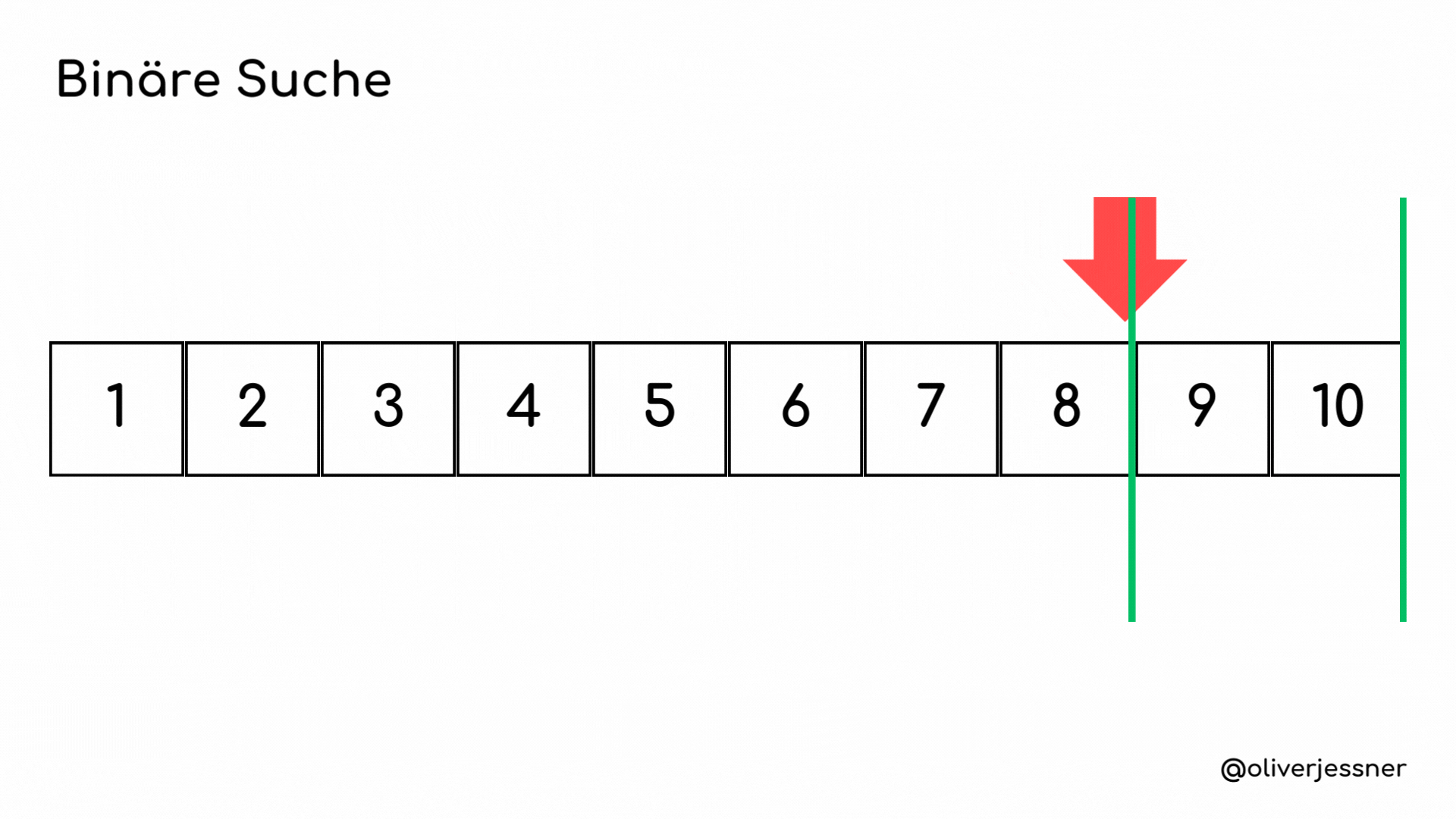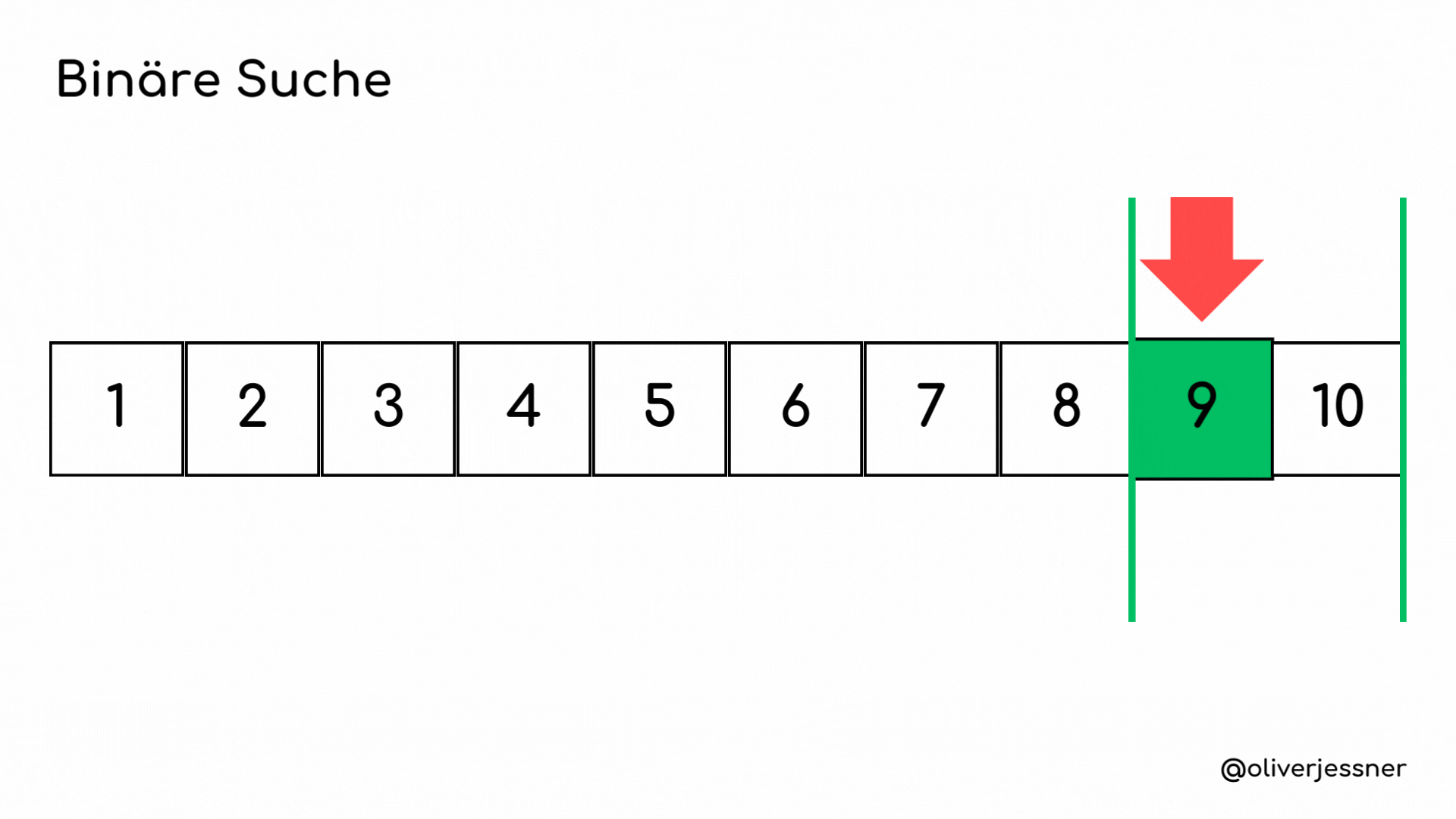
Die binäre Suche beginnt damit, die Mitte des Arrays zu ermitteln, was in unserem Fall die 5 ist. Die Mitte wird immer durch unseren roten Pfeil dargestellt.Der Algorithmus vergleicht nun das mittlere Element mit dem gesuchten Element. Wenn sie übereinstimmen, ist die Suche abgeschlossen. Falls das gesuchte Element größer ist als das mittlere Element, wissen wir, dass es sich nur im rechten Teil des Arrays befinden kann. Daher schließen wir den linken Teil aus. Wir ermitteln erneut die Mitte, diesmal im rechten Teil des Arrays, und haben dafür die 8 gefunden. Da das gesuchte Element immer noch größer als die Mitte ist, verkleinern wir unseren Suchbereich erneut. Wir ermitteln die Mitte des letzten Arrays und finden unsere 9.

Talk is cheap, show me code

Vollständigkeitshalber sehen wir uns den Code für die lineare/iterative Suche an:

const nums = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10];

for (let i = 0; i < nums.length - 1; i++) {
    if (nums[i] === 9) {
        console.log('Gefunden ' + i);
    }
}

Ich denke, das ist völlig klar. Lass uns einen Blick auf den Code der binären Suche werfen:

const nums = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10];

function binarySearch(arr, needle, start = 0, end = arr.length - 1) {
    const middle = Math.floor((start + end) / 2);

    if (needle === arr[middle]) {
        return middle;
    }
    if (start >= end) {
        return false; // -1
    }

    if (needle < arr[middle]) {
        return binarySearch(arr, needle, start, middle - 1);
    }

    return binarySearch(arr, needle, middle + 1, end);
}

console.log(binarySearch(nums, 9)); // 8
console.log(binarySearch(nums, 1)); // 0
console.log(binarySearch(nums, 10)); // 9
console.log(binarySearch(nums, 5)); // 4
console.log(binarySearch(nums, 11)); // false
console.log(binarySearch(nums, -1)); // false

Der Code zeigt uns, dass wir hier wunderbar Rekursion verwenden können, um unsere Teilarrays zu finden. Als Endrekursion gibt es zwei Möglichkeiten: einmal, wenn wir das Array gefunden haben, und einmal, wenn wir es nicht gefunden haben. Wenn wir ein Teilarray ansehen wollen, müssen wir nur entweder die rechte oder linke Seite des Arrays betrachten. Ist unsere gesuchte Zahl kleiner als die Mitte des Arrays, müssen wir das linke Teilarray durchsuchen. Ist die gesuchte Zahl größer als die Mitte, müssen wir das rechte Array durchsuchen.

Wo finden wir die Binäre suche?

Hier habe wieder ein paar Einsatzgebiete für euch aufgeschrieben:

• In Datenbanken werden oft Indizes auf sortierten Spalten erstellt, und der binäre Suchalgorithmus kann verwendet werden, um in diesen Indizes nach bestimmten Werten zu suchen.
• In Netzwerken kann der binäre Suchalgorithmus dazu verwendet werden, IP-Adressen oder andere Ressourcen in sortierten Listen zu suchen, was beispielsweise bei Routing- oder Load-Balancing-Algorithmen relevant sein kann.
• Auch in einigen Standardbibliotheken (STD libs) findet sich der binäre Suchalgorithmus.

Fazit

Ich habe bemerkt, dass viele Entwickler kein Wissen über solche Basics wie die binäre Suche haben, was sicherlich dem einen oder anderen nicht im Weg stehen wird. Jedoch verwehrt es den meisten die Möglichkeit, schwierigere und komplexere Probleme zu lösen.

PS: Hast du schon meinen Artikel über Stacks gelesen? Nein? Dann schau doch mal hier: Warum du etwas über Stacks lernen musst in 2024